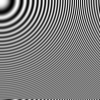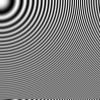画像の縮小処理におけるエイリアスの発生とそれを抑える仕組み

OpenGL+GLSLによる画像処理プログラミング―「OpenGL」と「シェーダ言語」で「レタッチ・ソフト」の仕組みを知る! (I・O BOOKS)

作者: 酒井幸市
出版社/メーカー: 工学社
発売日: 2009/11
メディア: 単行本
購入: 3人クリック: 10回
この商品を含むブログ (6件) を見る

　OpenGL使って画像処理をしたかったので参考に買ってみた。

　「OpenGLとシェーダ言語でレタッチ・ソフトの仕組みを知る！」って書いてあるけど、信号処理について全く知らない人が、よっしゃ画像処理やってみようっていって読める本ではない。重要な部分で説明が載ってなかったりする。で、パラパラめくってあぁそうだね、って言う人は、おそらくもうこれに載っている程度のことは大体知ってるだろう。

　それにしても、第二章にある縮小の項目は流石に説明がなさ過ぎる気がする。縮小の際のエイリアスについて言及しながら、それ以降の説明が、こういうフィルター通したらエイリアスだいぶ消えたでしょというだけで一切無いとか放置感がすごい。4章にて解説的な雰囲気を醸し出しておきながら、縮小については一切の説明がない。確かに、肝となる部分がp95 〜 101に書いてあるのだけど、普通わからん気がする。

　なので、ここで、画像を縮小すると何故エイリアスの問題が発生するのかについて、簡単に軽くてきとーに説明してみよう。

エイリアスと標本化定理

　標本化定理：ある周波数を表現するためには、その周波数の倍のサンプリングレートが必要である

　まぁ、波を表現するには最低限二点が必要というだけ。
　-(ハイフン)をいくら並べようと、「----」は波には見えないけど、_(アンダーバー)を混ぜれば、「-_-_」は波に見えるよね。

　エイリアスはこの定理を破ったときに現れる。この事は頭に置いておいて欲しい。

縮小とエイリアス

　画像を実空間で縮小すると、逆に周波数空間では拡大することになる。つまり、元画像では低周波領域だった周波数が高周波数領域になる。

　数学的に証明しなくても、縮小すると「間隔が狭くなる」＝「周期が短くなる」＝「周波数が高くなる」と当たり前のことを言ってるだけだ。

　ここで、全体的に高周波になること自体はなんの問題もない。（高周波はエイリアスではない。）

　では、いったい問題はなにか？

　ここでは、元の画像が、画像の持ち得る限界の周波数を含んでいた場合などを考えてみるとわかりやすい。
　この限界の周波数はサンプリング間隔（＝ピクセルの幅）に依存するので、表示するモニタが同じである以上、大きな画像だろうが、小さな画像だろうが変わらない。

　従って、縮小すると周波数は拡大するので、この画像の持つ限界の周波数帯は、画像を縮小するとその限界を超えてしまう。

　すなわち、エイリアスの発生である。
　なお、どの程度の周波数領域が縮小によって限界を超えてしまうかは、縮小倍率で変化する。（1/2に縮小するなら、限界の周波数/2までの周波数が超える）

　
　限界を超えてしまった周波数は折り返して低周波領域に現れてくる。こうなると、邪魔な低周波と元の低周波を分離することは不可能である。

　以下に例を示す。
（図1）
(図2)

　図２は図１を50％に線形補間で縮小した物である。線形補間ってローパスフィルタ（どんなフィルタの形なのかは知らんけど）だから多少は折り返す高周波を除去しているはずだが、それでも多くのエイリアスが発生しているのが分かる。

エイリアスの回避

　縮小によるエイリアスを回避するには、縮小する前に、問題を起こす高周波数領域をカット（ローパスフィルタをかける）すればよい。

　「OpenGL+GLSLによる画像処理プログラミング」にサンプルとして乗っているコードでは、縮小する前にはみ出して邪魔になる高周波領域を先にローパスフィルタを通して除去してから、線形補間で縮小している。

　最も単純なローパスフィルタは単に周波数空間に矩形関数をかけるだけだ。これを逆フーリエ変換して実空間にすると、sinc関数の畳み込みになる。
　このsinc関数は振動して0に収束しないので、無限遠までたたみ込まないといけない。計算機上それは不可能なので、窓関数をsinc関数にかけて、ある一定の範囲だけ値を持ち、その他は全て0になるようにする。
　窓関数は単純に矩形関数でも良いが、矩形関数は分解能がよろしくないので、ハン窓関数を使う。（窓関数(Wikipedia)）

（図3）